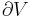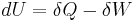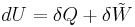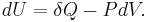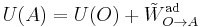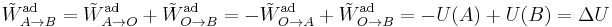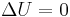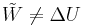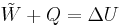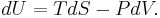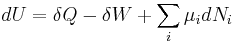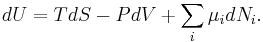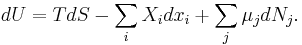First law of thermodynamics

Thermodynamics

Branches
Classical · Statistical · Chemical Equilibrium / Non-equilibrium Thermofluids

Laws
Zeroth · First · Second · Third

Systems
State: Equation of state Ideal gas · Real gas Phase of matter · Equilibrium Control volume · Instruments Processes: Isobaric · Isochoric · Isothermal Adiabatic · Isentropic · Isenthalpic Quasistatic · Polytropic Free expansion Reversibility · Irreversibility Endoreversibility Cycles: Heat engines · Heat pumps Thermal efficiency

System properties
Property diagrams Intensive and extensive properties State functions: Temperature / Entropy (intro.) † Pressure / Volume † Chemical potential / Particle no. † († Conjugate variables) Vapor quality Reduced properties Process functions: Work · Heat

Material properties

Specific heat capacity

$c=$

$T$	$\partial S$
$N$	$\partial T$

Compressibility

$\beta=-$

$1$	$\partial V$
$V$	$\partial p$

Thermal expansion

$\alpha=$

$1$	$\partial V$
$V$	$\partial T$

Property database

Equations
Carnot's theorem Clausius theorem Fundamental relation Ideal gas law Maxwell relations Table of thermodynamic equations

Potentials

Free energy · Free entropy

Internal energy	$U(S,V)$
Enthalpy	$H(S,p)=U+pV$
Helmholtz free energy	$A(T,V)=U-TS$
Gibbs free energy	$G(T,p)=H-TS$

History and culture

Philosophy:
Entropy and time · Entropy and life
Brownian ratchet
Maxwell's demon
Heat death paradox
Loschmidt's paradox
Synergetics

History:
General · Heat · Entropy · Gas laws
Perpetual motion
Theories:
Caloric theory · Vis viva
Theory of heat
Mechanical equivalent of heat
Motive power
Publications:
"An Experimental Enquiry Concerning ... Heat"
"On the Equilibrium of Heterogeneous Substances"
"Reflections on the
Motive Power of Fire"

Timelines of:
Thermodynamics · Heat engines

Art:
Maxwell's thermodynamic surface

Education:
Entropy as energy dispersal

Scientists
Daniel Bernoulli Sadi Carnot Benoît Paul Émile Clapeyron Rudolf Clausius Hermann von Helmholtz Julius Robert von Mayer William Rankine John Smeaton Georg Ernst Stahl Benjamin Thompson William Thomson John James Waterston

The first law of thermodynamics, an expression of the principle of conservation of energy, states that energy can be transformed (changed from one form to another), but cannot be created or destroyed. It is usually formulated by saying that the change in the internal energy of a system is equal to the amount of heat supplied to the system, minus the amount of work done by the system on its surroundings.

1 Description
2 Classical Statement
- 2.1 Adiabatic processes
- 2.2 Non adiabatic processes
3 Mathematical formulation
4 See also
5 Notes and references
6 Further reading
7 External links

Description

The first law of thermodynamics says that energy is conserved in any process involving a thermodynamic system and its surroundings. Frequently it is convenient to focus on changes in the assumed internal energy (U) and to regard them as due to a combination of heat (Q) added to the system and work done by the system (W). Taking 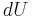$dU$ as an infinitesimal (differential) change in internal energy, one writes

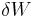$dU = \delta Q - \delta W\,$

where $\delta Q$ and $\delta W$ are infinitesimal amounts of heat supplied to the system and work done by the system, respectively. Note that the minus sign in front of 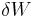$\delta W$ indicates that a positive amount of work done by the system leads to energy being lost from the system.

Depending on discipline, an alternative convention may be adopted for the "work" under consideration, leading to:

$dU = \delta Q + \delta \tilde{W}\,$

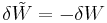where $\delta \tilde{W}= -\delta W$ is the work done on the system by the surroundings.^[1]

When a system expands in a quasistatic process, the work done on the system is 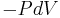$-PdV$ whereas the work done by the system while expanding is 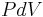$PdV$ . In any case, both give the same result when written explicitly as:

$dU=\delta Q-PdV.\,$

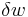Work and heat are due to processes which add or subtract energy, while U is a particular form of energy associated with the system. Thus the term "heat energy" for $\delta Q$ means "that amount of energy added as the result of heating" rather than referring to a particular form of energy. Likewise, "work energy" for $\delta w$ means "that amount of energy lost as the result of work". Internal energy is a property of the system whereas work done and heat supplied are not. A significant result of this distinction is that a given internal energy change (dU) can be achieved by, in principle, many combinations of heat and work.

Informally, the law was first formulated by Germain Hess via Hess's Law, and later by Julius Robert von Mayer^[2]

Classical Statement

The first explicit statement of the first law of thermodynamics was given by Rudolf Clausius in 1850: "There is a state function E, called ‘energy’, whose differential equals the work exchanged with the surroundings during an adiabatic process."

Adiabatic processes

The classical statement of the first law of thermodynamics is induced from empirical evidence. It can be observed that given a system in an initial state, if work is exerted on the system in an adiabatic (i.e. thermally insulated) way, the final state is the same for a given amount of work, irrespective of how this work is performed.

For instance, in Joule's experiment, the initial system is a tank of water with a paddle wheel inside. If we isolate thermally the tank and move the paddle wheel with a pulley and a weight we can relate the increase in temperature with the height descended by the mass. Now the system is returned to its initial state, isolated again, and the same amount of work is done on the tank using different devices (an electric motor, a chemical battery, a spring,...). In every case, the amount of work can be measured independently. The evidence shows that the final state of the water (in particular, its temperature) is the same in every case. It's irrelevant if the work is electrical, mechanical, chemical,... or if done suddenly or slowly, as long as it is performed in an adiabatic way.

This evidence leads to the classical statement of the first law of thermodynamics

For all adiabatic processes between two specified states of a closed system, the net work done is the same regardless of the nature of the closed system and the details of the process.

This affirmation of path independence allows to define a state function, named internal energy, $U$ , as the adiabatic work necessary to go from a reference state to a given one

$U(A)=U(O) + \tilde{W}^\mathrm{ad}_{O\to A}$

where, following IUPAC convention we take as positive the work done on the system.

To go from a state A to a state B we can take a path that goes through the reference state, since the adiabatic work is independent of the path

$\tilde{W}^\mathrm{ad}_{A\to B}=\tilde{W}^\mathrm{ad}_{A\to O}+\tilde{W}^\mathrm{ad}_{O\to B} = -\tilde{W}^\mathrm{ad}_{O\to A}+\tilde{W}^\mathrm{ad}_{O\to B} = -U(A) + U(B) = \Delta U$

In particular, if no work is exerted on a thermally isolated system we have

$\Delta U = 0\,$

or, in words,

The internal energy of an isolated system remains constant.

This is the law of conservation of energy.

Non adiabatic processes

When the system evolves in a non adiabatic way, it is observed that the work exerted on the system does not coincide with the increase in its internal energy (that, being a state function, can be used for both adiabatic and non adiabatic processes).

$\tilde{W}\neq \Delta U$

The difference is interpreted in terms of the heat that enters in the system, so the inequality can be transformed in an equality as

$\tilde{W} + Q = \Delta U\,$

This is the usual expression the first law of thermodynamics. The inclusion of an unknown term (heat) does not transform it in a tautology, since its real physicial content lies in the fact that there exists a state function that can be calculated independently of heat and work.

Mathematical formulation

The infinitesimal heat and work in the equations above are denoted by δ rather than d because, in mathematical terms, they are not exact differentials. In other words, they do not describe the state of any system. The integral of an inexact differential depends upon the particular "path" taken through the space of thermodynamic parameters while the integral of an exact differential depends only upon the initial and final states. If the initial and final states are the same, then the integral of an inexact differential may or may not be zero, but the integral of an exact differential will always be zero. The path taken by a thermodynamic system through a chemical or physical change is known as a thermodynamic process.

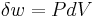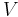An expression of the first law can be written in terms of exact differentials by realizing that the work that a system does is, in case of a reversible process, equal to its pressure times the infinitesimal change in its volume. In other words $\delta w=PdV$ where $P$ is pressure and $V$ is volume. Also, for a reversible process, the total amount of heat added to a system can be expressed as 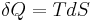$\delta Q=TdS$ where $T$ is temperature and $S$ is entropy. Therefore, for a reversible process:

$dU=TdS-PdV.\,$

Since U, S and V are thermodynamic functions of state, the above relation holds also for non-reversible changes. The above equation is known as the fundamental thermodynamic relation.

In the case where the number of particles in the system is not necessarily constant and may be of different types, the first law is written:

$dU=\delta Q-\delta W + \sum_i \mu_i dN_i\,$

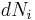where $dN_i$ is the (small) number of type-i particles added to the system, and 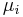$\mu_i$ is the amount of energy added to the system when one type-i particle is added, where the energy of that particle is such that the volume and entropy of the system remains unchanged. 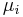$\mu_i$ is known as the chemical potential of the type-i particles in the system. The statement of the first law, using exact differentials is now:

$dU=TdS-PdV + \sum_i \mu_i dN_i.\,$

If the system has more external variables than just the volume that can change, the fundamental thermodynamic relation generalizes to:

$dU = T dS - \sum_{i}X_{i}dx_{i} + \sum_{j}\mu_{j}dN_{j}.\,$

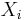Here the $X_{i}$ are the generalized forces corresponding to the external variables $x_{i}$ .

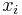A useful idea from mechanics is that the energy gained by a particle is equal to the force applied to the particle multiplied by the displacement of the particle while that force is applied. Now consider the first law without the heating term: 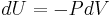$dU=-PdV$ . The pressure P can be viewed as a force (and in fact has units of force per unit area) while dV is the displacement (with units of distance times area). We may say, with respect to this work term, that a pressure difference forces a transfer of volume, and that the product of the two (work) is the amount of energy transferred as a result of the process.

It is useful to view the TdS term in the same light: With respect to this heat term, a temperature difference forces a transfer of entropy, and the product of the two (heat) is the amount of energy transferred as a result of the process. Here, the temperature is known as a "generalized" force (rather than an actual mechanical force) and the entropy is a generalized displacement.

Similarly, a difference in chemical potential between groups of particles in the system forces a transfer of particles, and the corresponding product is the amount of energy transferred as a result of the process. For example, consider a system consisting of two phases: liquid water and water vapor. There is a generalized "force" of evaporation which drives water molecules out of the liquid. There is a generalized "force" of condensation which drives vapor molecules out of the vapor. Only when these two "forces" (or chemical potentials) are equal will there be equilibrium, and the net transfer will be zero.

The two thermodynamic parameters which form a generalized force-displacement pair are termed "conjugate variables". The two most familiar pairs are, of course, pressure-volume, and temperature-entropy.

Notes and references

↑ This is the convention adopted by essentially all modern textbooks of physical chemistry, such as those by Peter Atkins and Ira Levine, but many textbooks on physics define work by default as work done by the system.
↑ Mayer, Robert (1841). Paper: 'Remarks on the Forces of Nature"; as quoted in: Lehninger, A. (1971). Bioenergetics - the Molecular Basis of Biological Energy Transformations, 2nd. Ed. London: The Benjamin/Cummings Publishing Company.

External links

MISN-0-158, The First Law of Thermodynamics (PDF file) by Jerzy Borysowicz for Project PHYSNET.
First law of thermodynamics in the MIT Course Unified Thermodinamics and Propulsion from Prof. Z. S. Spakovszky